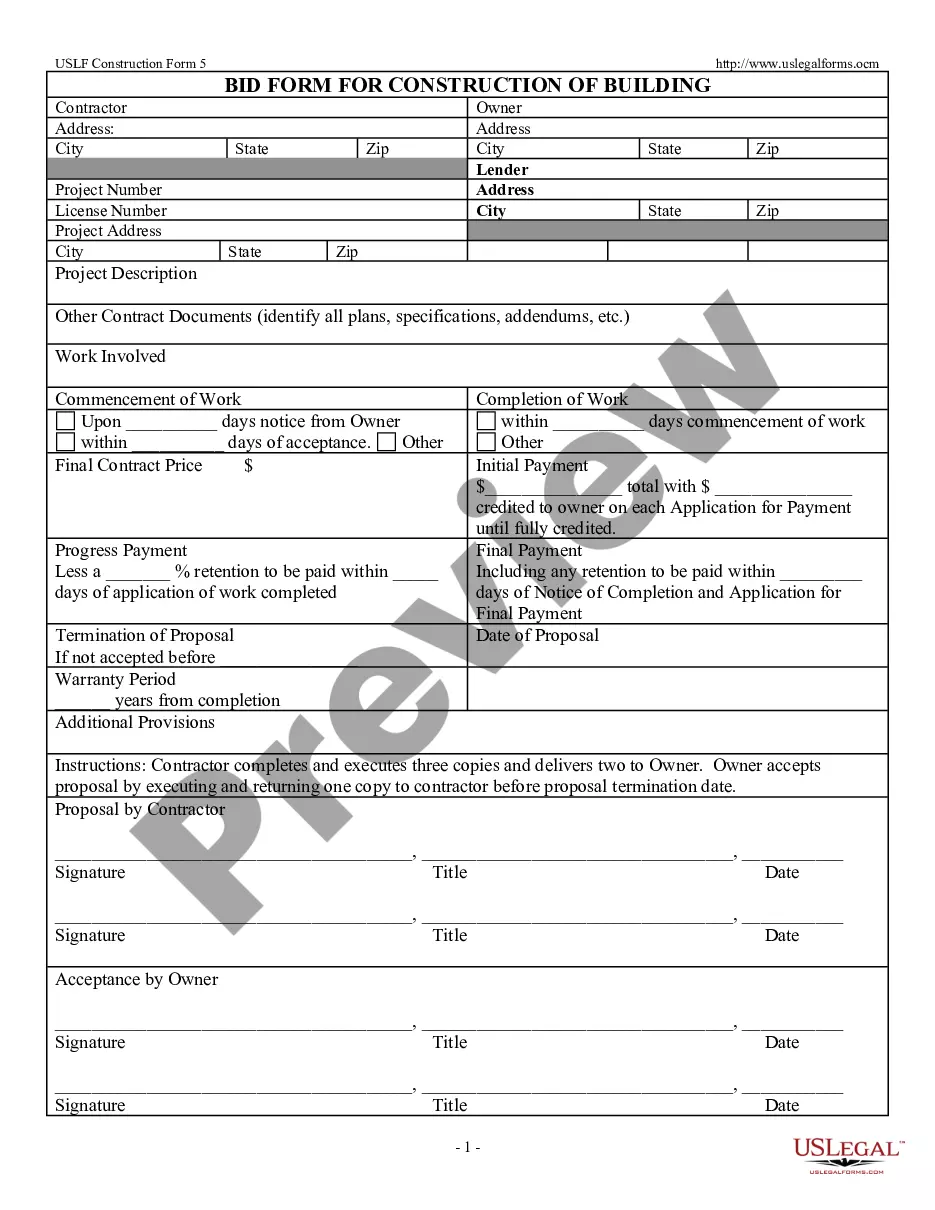
Calculator With Bar Notation In Nassau
Description
Form popularity
FAQ
You take the numerator. 1 divided by the bottom the denominator. So 1 divided by 3 is going to giveMoreYou take the numerator. 1 divided by the bottom the denominator. So 1 divided by 3 is going to give us this. Now notice the reason why you use bar notation is when you get decimals that repeat.
A bar can be given to the numbers that are being repeated only after a decimal point and not before a decimal point. Example: 1) 77.7 can be written as it is, like 77.7. 2) 7.77... cannot be written as 7.77... a bar notation can be used to represent the repeating number.
Because both of them repeat. So that's how you would write 0.36 repeating using bar notation on toMoreBecause both of them repeat. So that's how you would write 0.36 repeating using bar notation on to number three where we have point eight three and the three is repeating.
Because both of them repeat. So that's how you would write 0.36 repeating using bar notation on toMoreBecause both of them repeat. So that's how you would write 0.36 repeating using bar notation on to number three where we have point eight three and the three is repeating. Not the eight.
A bar notation is a line over a number. When a number or a group of numbers are repeated, this is the term to employ.
In bar notation, a bar is placed over the digit or digits that are repeated. In this case, the number 1.0929292... would be expressed as 1.092. Bar notation is a simple and convenient way to represent repeating decimal numbers.
In this example, the digits 2.1777 repeat infinitely, so they are written as 2.1777¯.
Answer: 2.261 with the bar notation line over 61.